Educational Activities and Resources
Courses that I currently teach
This laboratory course is intended primarily for advanced Biology and Chemistry majors. The course focuses on methods for isolating and characterizing proteins, including chromatography, electrophoresis and enzyme kinetics. Quantitative analysis is strongly emphasized, and computers are used extensively for collecting and analyzing data, as well as molecular modeling.
Most of the experiments in the course utilize the well-characterized enzyme trypsin, a member of the serine protease family. Trypsin, is presently one of the best understood enzymes, and it offers many opportunities to illustrate important general principles in biochemistry. This course is offered during the spring semester. There is one laboratory session per week (with sections on Monday, Tuesday, Wednesday and Thursday afternoons) and one lecture, on Thursday mornings from 9:40 to 10:30 AM.
Most of the experiments in the course utilize the well-characterized enzyme trypsin, a member of the serine protease family. Trypsin, is presently one of the best understood enzymes, and it offers many opportunities to illustrate important general principles in biochemistry. This course is offered during the spring semester. There is one laboratory session per week (with sections on Monday, Tuesday, Wednesday and Thursday afternoons) and one lecture, on Thursday mornings from 9:40 to 10:30 AM.
Biology 3550 (previously 3820) is an interdisciplinary course designed to highlight the many connections between the physical and biological sciences. The course is intended for undergraduate majors in any of the sciences:
- Biology majors can expect to learn how the principles they have learned in chemistry, math and physics classes can lead to a deeper understanding of biological processes.
- Majors in the physical sciences will learn about new and challenging applications for their disciplines.
- Biology 3550 satisfies graduation requirements for:
- Biology major
- Chemistry major (Biological Chemistry track)
- Physics major (Medical Physics track, as a substitute for PHYS 3110)
- Students from other disciplines are also welcome! (See the list of prerequisites below.)
- Probability
- Random walks and diffusion
- Energy and thermodynamics
- Molecular motors
- And more!
- BIOL 2020 or BIOL 2021
- Chem 1229 or Chem 1221
- MATH 1180 or MATH 1220
- Recommended: PHYS 2020 or PHYS 2120 or PHYS 2220 or PHYS 3220
NMR Pedagogy
Having come to NMR spectroscopy rather late in life, I have been particularly interested in understanding the underlying principles of the technique and in finding ways to more effectively teach these principles. Although some basic aspects of NMR can be understood using analogies to macroscopic phenomena (especially the precession of spinning objects, like a gyroscope), other features are based on quantum-mechanical phenomena that do not have simple analogies in our everyday experience. This is particularly true of multi-dimensional NMR experiments that reflect the coupling of nuclei through covalent bonds (scalar coupling). While these experiments are central to modern biomolecular NMR, understanding them is challenging for nearly everyone. Mathematical tools, including the density matrix and the product operator formalism, allow us to accurately describe experiments and their outcomes, but these tools represent a high degree of abstraction that may obscure the underlying physical phenomena.
In the hopes of making a deeper understanding of NMR accessible to students with backgrounds in, for instance, chemistry and biochemistry, I have written a text book targeted to this audience, Principles of NMR Spectroscopy: An illustrated guide. After a very long gestation the book was published in 2016 by University Science Books. Additional information about the book, including electronic supplements, can be found here.
A more condensed presentation of the treatment of scalar coupling has been published in Concepts in Magnetic Resonance:
Goldenberg, D. P. (2010). The product operator formalism: A physical and graphical interpretation. Concepts Magn. Reson. Part A., 36A, 49–83. http://dx.doi.org/10.1002/cmr.a.20156
This paper emphasizes the role of quantum correlations between scalar-coupled spins and introduces a novel (so far as I know) style of vector diagram to help illustrate these correlations and their interconversion with observable magnetization. For instance, the diagram below represents a correlation between the z-magnetization components of two spins (labeled, as usual, "I" and "S"):
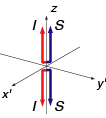
The diagram is meant to indicate that if the z-magnetization of the I -spin is measured and observed to be positive, the z-magnetization of the S-spin will also be positive. Importantly, the correlation is a property distinct from the observable magnetization components of the individual spins and can exist even when the spin pair is in a superposition state for which the z-magnetization components of both spins are indeterminate. For a population of spin-pairs, the average contribution of this correlation is represented by the IzSz product-operator component of the density matrix.
The vector diagrams can be used to describe the effects of pulses and evolution periods, extending the classical treatment of single-spin systems. The diagram below illustrates the effect of a selective π/2 pulse to the I-spin, converting the IzSz correlation to an IxSz correlation:
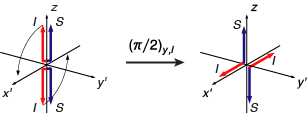
As with the IzSz correlation, IxSz is not associated with any net magnetization components. However, this correlation can evolve with time, under the influence of the scalar coupling interaction, into observable magnetization, as illustrated by the diagram below:
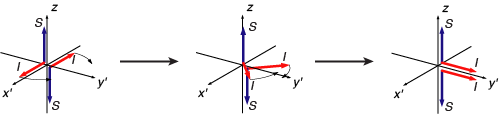
The two vectors representing the I-spin are visualized as precessing at different frequencies, reflecting the spin-up or spin-down states of the coupled S-spin. When the vectors meet at the y'-axis, there is a net observable magnetization in that direction. It is important to stress, however, that these effects do not necessarily reflect different spin pairs in which, for instance, the I-spin is coupled to either a spin-up or spin-down S-spin. A population of spins can, in principle, all be in the same quantum state and give rise to two precession frequencies and the interconversion illustrated above. This is a very mysterious business that is due to the "entanglement" of the two spins. Much has been written about quantum entanglement and new applications in cryptography and computing, but NMR spectroscopists already utilize it every day! Indeed, nearly all of the multi-dimensional experiments used for biomolecular NMR rely at their core on these phenomena.
For a full discussion and numerous examples of the diagrams, see the Concepts in Magnetic Resonance paper.
There is also a Mathematica appendix to the paper, including a general libraries of functions for spin-1/2 quantum calculations, which can be downloaded here or from the publisher's's web page. The version here includes a slightly updated version of the libraries.
Cautionary note:
Rather unfortunately, the Concepts in Magnetic Resonance article was written using the "left-hand rule" convention for describing the direction of rotations. At the time, I favored that convention because it was consistent with most earlier books that relied on vector diagrams. While completing the textbook, I was finally convinced that the "right-hand" convention is more internally consistent and has been adopted in nearly all newer books and articles. The book, therefore, follows the more modern right-hand convention.
In the hopes of making a deeper understanding of NMR accessible to students with backgrounds in, for instance, chemistry and biochemistry, I have written a text book targeted to this audience, Principles of NMR Spectroscopy: An illustrated guide. After a very long gestation the book was published in 2016 by University Science Books. Additional information about the book, including electronic supplements, can be found here.
A more condensed presentation of the treatment of scalar coupling has been published in Concepts in Magnetic Resonance:
Goldenberg, D. P. (2010). The product operator formalism: A physical and graphical interpretation. Concepts Magn. Reson. Part A., 36A, 49–83. http://dx.doi.org/10.1002/cmr.a.20156
This paper emphasizes the role of quantum correlations between scalar-coupled spins and introduces a novel (so far as I know) style of vector diagram to help illustrate these correlations and their interconversion with observable magnetization. For instance, the diagram below represents a correlation between the z-magnetization components of two spins (labeled, as usual, "I" and "S"):

The diagram is meant to indicate that if the z-magnetization of the I -spin is measured and observed to be positive, the z-magnetization of the S-spin will also be positive. Importantly, the correlation is a property distinct from the observable magnetization components of the individual spins and can exist even when the spin pair is in a superposition state for which the z-magnetization components of both spins are indeterminate. For a population of spin-pairs, the average contribution of this correlation is represented by the IzSz product-operator component of the density matrix.
The vector diagrams can be used to describe the effects of pulses and evolution periods, extending the classical treatment of single-spin systems. The diagram below illustrates the effect of a selective π/2 pulse to the I-spin, converting the IzSz correlation to an IxSz correlation:

As with the IzSz correlation, IxSz is not associated with any net magnetization components. However, this correlation can evolve with time, under the influence of the scalar coupling interaction, into observable magnetization, as illustrated by the diagram below:

The two vectors representing the I-spin are visualized as precessing at different frequencies, reflecting the spin-up or spin-down states of the coupled S-spin. When the vectors meet at the y'-axis, there is a net observable magnetization in that direction. It is important to stress, however, that these effects do not necessarily reflect different spin pairs in which, for instance, the I-spin is coupled to either a spin-up or spin-down S-spin. A population of spins can, in principle, all be in the same quantum state and give rise to two precession frequencies and the interconversion illustrated above. This is a very mysterious business that is due to the "entanglement" of the two spins. Much has been written about quantum entanglement and new applications in cryptography and computing, but NMR spectroscopists already utilize it every day! Indeed, nearly all of the multi-dimensional experiments used for biomolecular NMR rely at their core on these phenomena.
For a full discussion and numerous examples of the diagrams, see the Concepts in Magnetic Resonance paper.
There is also a Mathematica appendix to the paper, including a general libraries of functions for spin-1/2 quantum calculations, which can be downloaded here or from the publisher's's web page. The version here includes a slightly updated version of the libraries.
Cautionary note:
Rather unfortunately, the Concepts in Magnetic Resonance article was written using the "left-hand rule" convention for describing the direction of rotations. At the time, I favored that convention because it was consistent with most earlier books that relied on vector diagrams. While completing the textbook, I was finally convinced that the "right-hand" convention is more internally consistent and has been adopted in nearly all newer books and articles. The book, therefore, follows the more modern right-hand convention.